Quadrato (algebra)

In algebra, viene definito quadrato di un numero ${\displaystyle x}$ l'elevamento dello stesso alla seconda potenza, ossia la sua moltiplicazione per sé stesso eseguita una volta:

${\displaystyle x^{2}=x\cdot x.}$

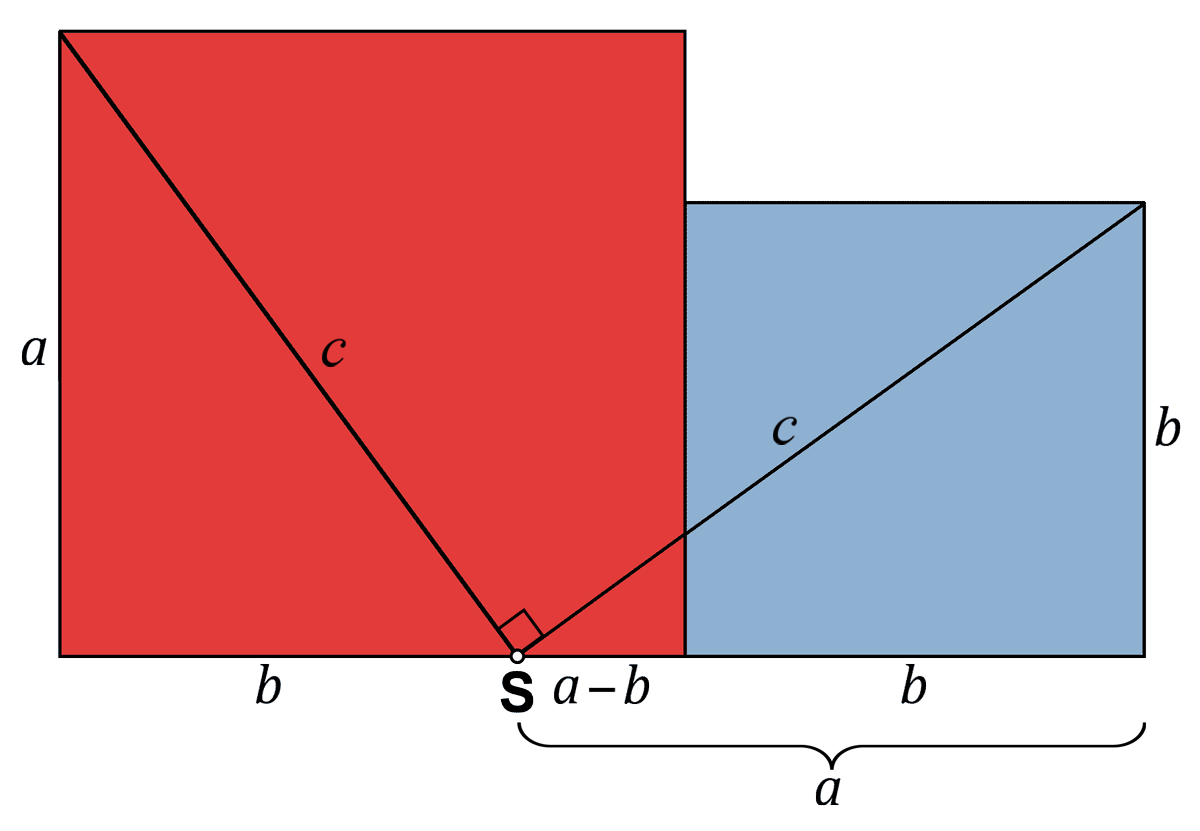
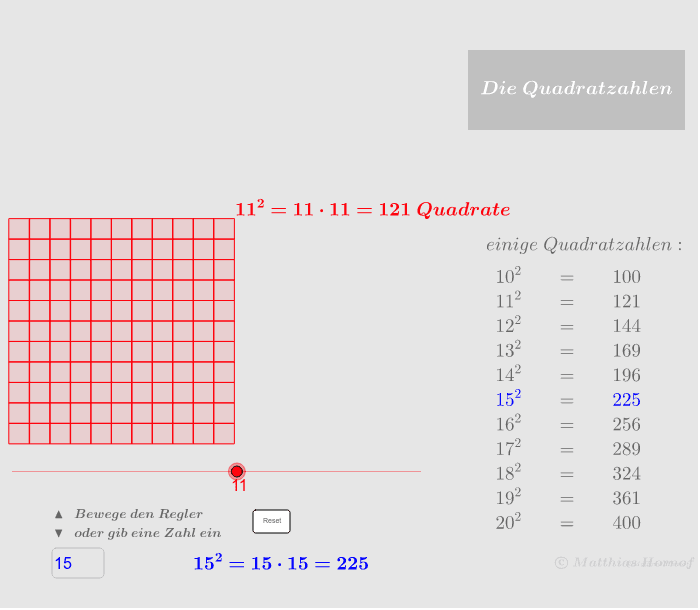
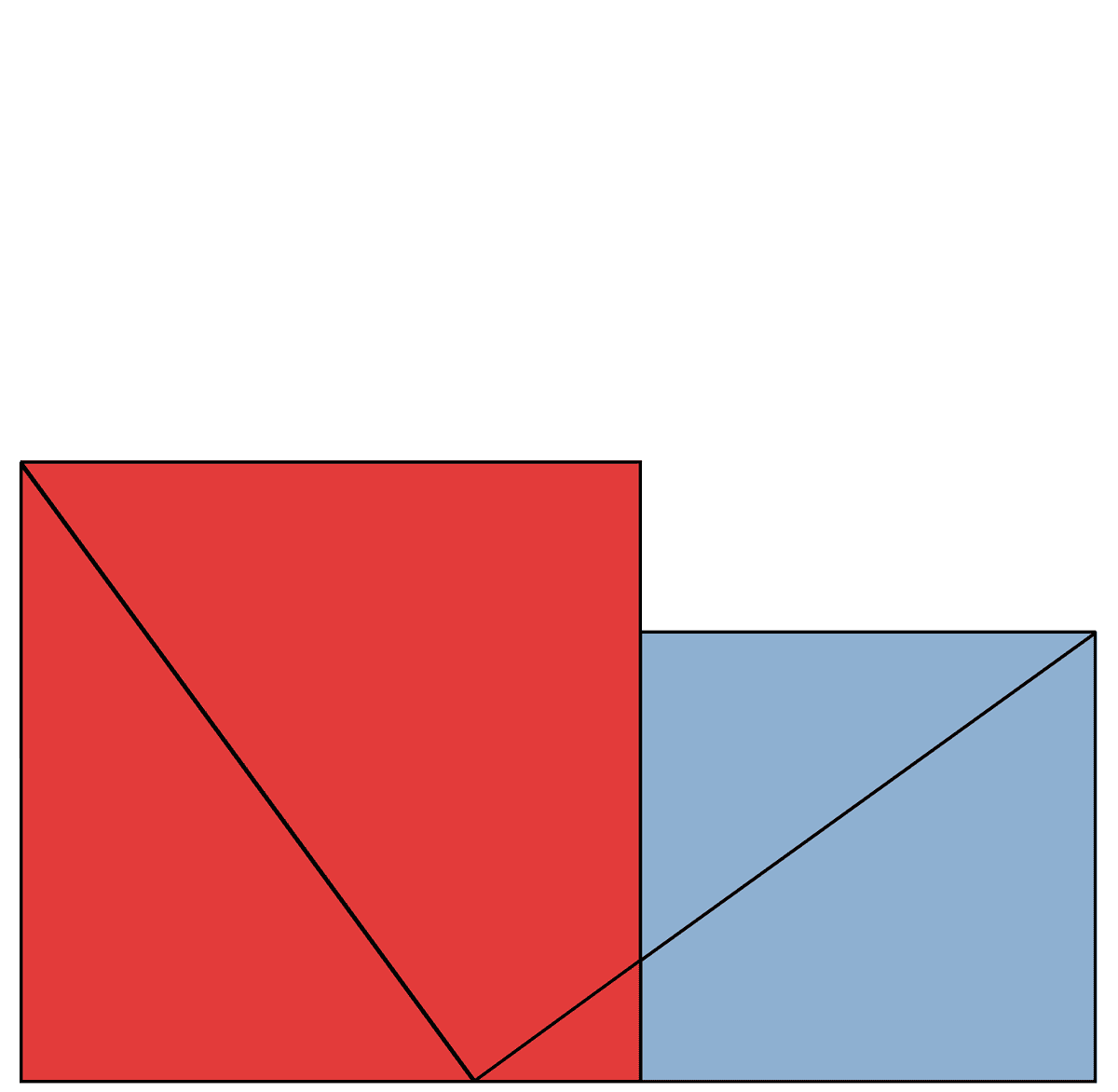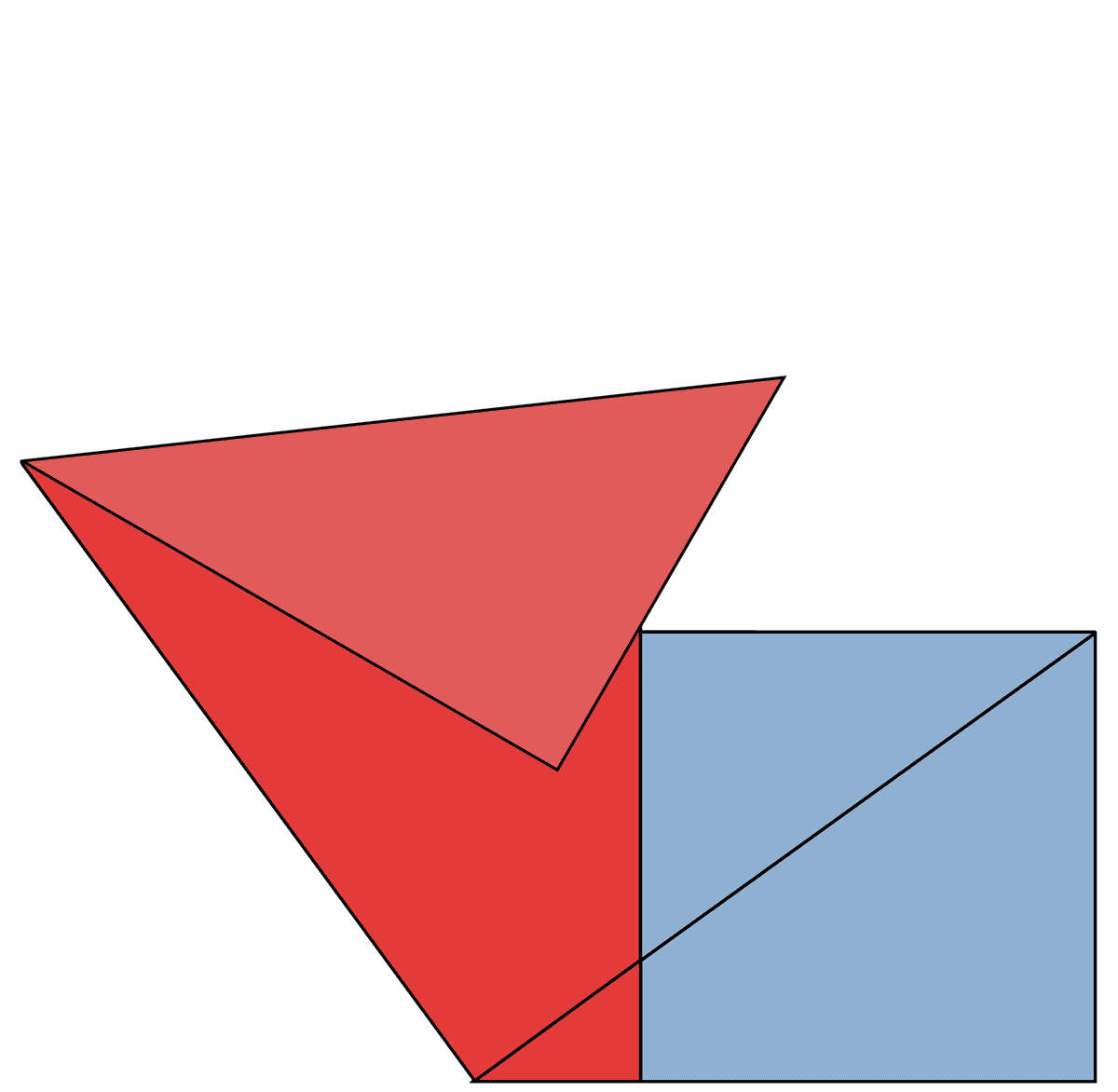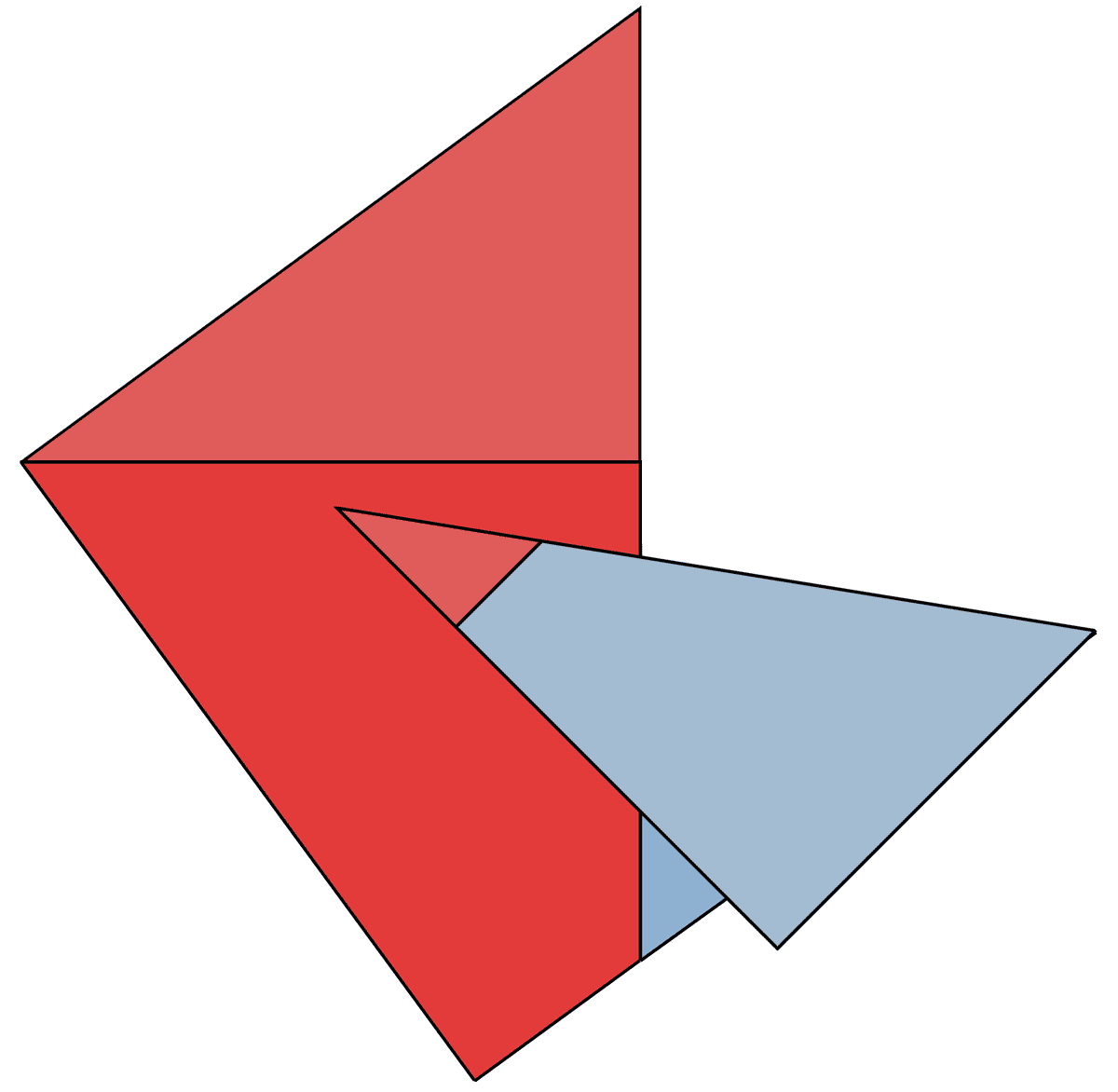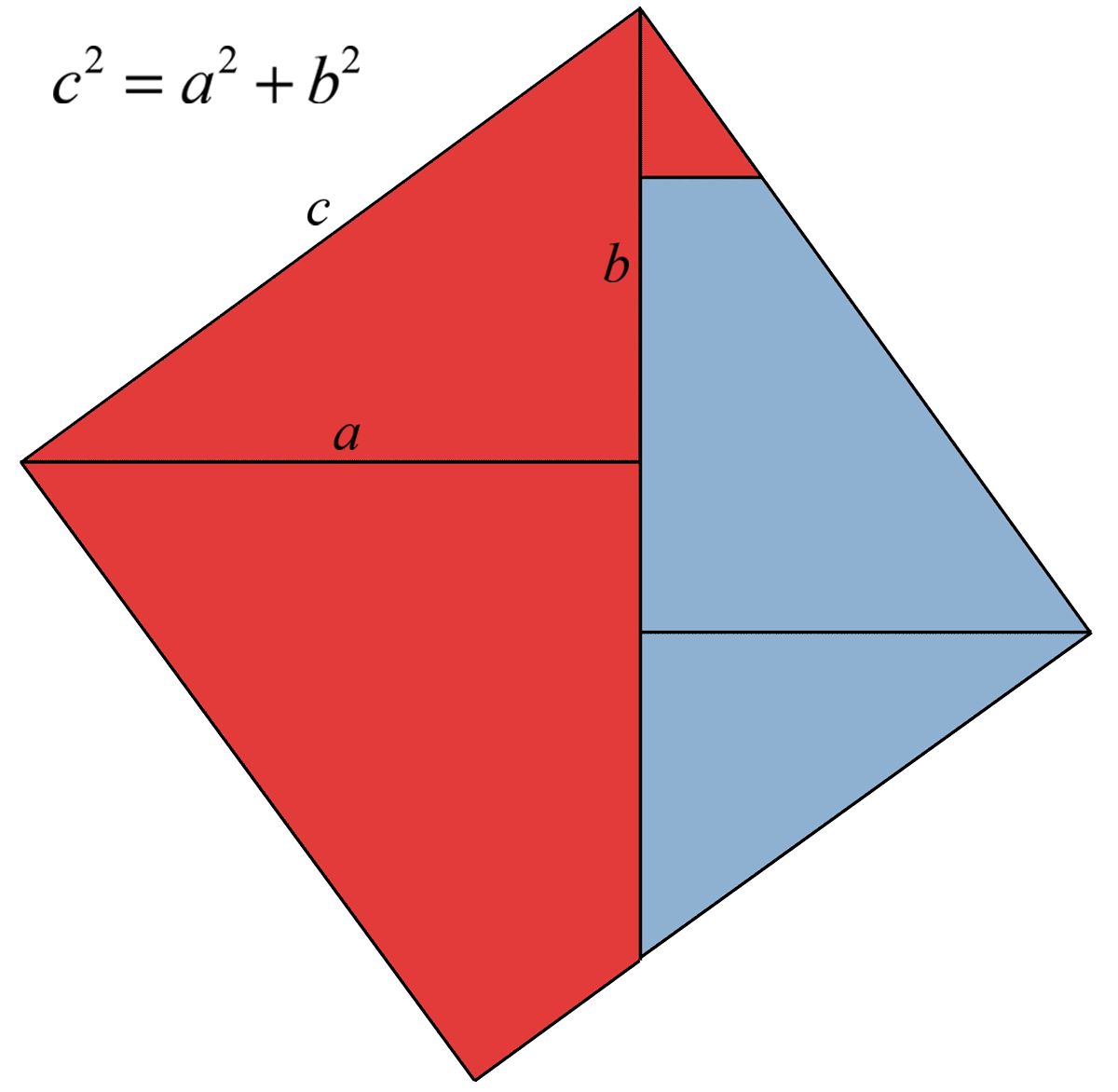
Il termine quadrato viene dalla geometria, poiché l'area di un quadrato si ottiene appunto moltiplicando il lato per sé stesso.

Il quadrato di un numero immaginario è un numero reale minore o uguale a zero, mentre per i numeri complessi si calcola

${\displaystyle \left(a ib\right)^{2}=a^{2}-b^{2} i\cdot 2ab.}$

Proprietà

• Il quadrato di un numero reale è sempre maggiore o uguale a zero, dato che il prodotto di valori con lo stesso segno è sempre positivo. Quindi

${\displaystyle x^{2}\geq 0\qquad \forall x\in \mathbb {R} .}$

• Per lo stesso motivo vale la relazione

${\displaystyle x^{2}=\left(-x\right)^{2}.}$

Ad esempio il quadrato di ${\displaystyle 2}$ è ${\displaystyle 4}$, ma anche il quadrato di ${\displaystyle -2}$ è uguale a ${\displaystyle 4}$.

• Il quadrato di un numero immaginario è sempre minore di zero, perché elevando al quadrato l'unità immaginaria si ottiene un numero negativo, che si moltiplica poi con il quadrato del coefficiente (che è positivo).
• la somma dei numeri dispari in ordine è un quadrato perfetto di un numero pari o dispari (proprietà nota al matematico greco Euclide):

${\displaystyle 1=1^{2}}$

${\displaystyle 1 3=2^{2}}$

${\displaystyle 1 3 5=3^{2}}$

${\displaystyle 1 3 5 7=4^{2}}$

${\displaystyle 1 3 5 7 9=5^{2}}$, da cui:

${\displaystyle 1^{2}=1}$

${\displaystyle 2^{2}=1^{2} 3}$

${\displaystyle 3^{2}=2^{2} 5}$

${\displaystyle 4^{2}=3^{2} 7}$

${\displaystyle 5^{2}=4^{2} 9}$

${\displaystyle n^{2}=(n-1)^{2} 2n-1}$ che risolta porta, infatti, ad una identità.

Da una formula siffatta si identificano un sottoinsieme infinito numerabile delle terne pitagoriche, per ogni ${\displaystyle {\sqrt {2n-1}}}$ intero. Ad es. : (3, 4, 5) con ${\displaystyle n=5}$; (5, 12 ,13); (7, 24 ,25); (9, 40, 41); (11, 60, 61); (13, 84, 85); (15, 112, 113); (17, 144, 145); (19, 180, 181); (21, 220, 221); (23, 264, 265).

Quadrati perfetti

Il quadrato di un numero intero diverso da zero è sempre un numero naturale. I numeri naturali che sono quadrati di numeri interi si definiscono quadrati perfetti. Di seguito alcune proprietà:

• Il quadrato di un qualsiasi numero intero ${\displaystyle n}$ può essere rappresentato anche dalla somma

${\displaystyle 1 1 2 2 \ldots (n-1) (n-1) n.}$

Ad esempio

${\displaystyle 4^{2}=1 1 2 2 3 3 4=16.}$

• Il quadrato di un qualsiasi numero intero ${\displaystyle n}$ è inoltre uguale alla somma dei primi ${\displaystyle n}$ numeri dispari:

${\displaystyle 5^{2}=1 3 5 7 9=25}$

indicabile attraverso la formula

${\displaystyle n^{2}=\sum _{k=0}^{n-1}2k 1.}$

• Il quadrato di un qualsiasi numero intero ${\displaystyle n}$ è inoltre uguale alla somma del numero ${\displaystyle n}$ e dei primi ${\displaystyle n-1}$ numeri pari:

${\displaystyle 5^{2}=5 2 4 6 8=25}$

indicabile attraverso la formula

${\displaystyle n^{2}=n \sum _{k=1}^{n-1}2k.}$

• La somma dei quadrati dei primi n numeri naturali vale

${\displaystyle \sum _{k=1}^{n}k^{2}={\frac {n(n 1)(2n 1)}{6}}={\frac {2n^{3} 3n^{2} n}{6}}.}$

Voci correlate

• Numero quadrato
• Quadrato (geometria)
• Cubo
• Potenza (matematica)
• Radice quadrata
• Potenza di due

Altri progetti

• Wikizionario contiene il lemma di dizionario «quadrato»
• Wikimedia Commons contiene immagini o altri file sul quadrato